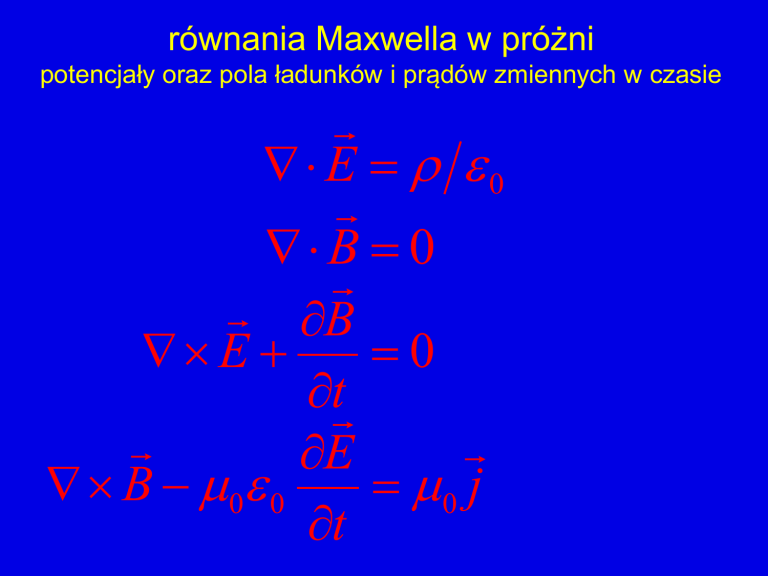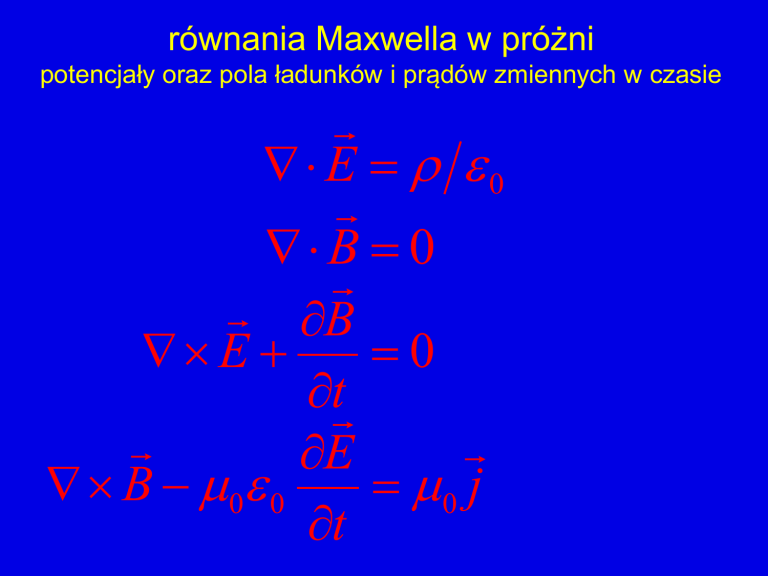
równania Maxwella w próżni
potencjały oraz pola ładunków i prądów zmiennych w czasie
E 0
B 0
B
E
0
t
E
B 0 0
0 j
t
płaska fala elektromagnetyczna w próżni
E (r , t ) E0 cos(k r t )
B(r , t ) B0 cos(k r t )
E
B 0 0
t
B
E
t
summa: energia, pęd, moment pędu
pola elektromagnetycznego
gęstość energii pola
elektromagnetycznego
wektor Poyntinga pola
elektromagnetycznego
u EM
0
2
E
1
S
( E B)
gęstość pędu pola
p
EM
elektromagnetycznego
lEM r pEM
1
2
20
B
2
0
0 0 S 0 ( E B)
0 (r ( E B))
gęstość momentu pędu pola elektromagnetycznego
po co to wszystko? : promieniowanie, teoria pola, kwanty
przykład: ciśnienie promieniowania
energia i pęd fali elektromagnetycznej
demo: radiometr Crooksa
przykład: ciśnienie promieniowania
energia i pęd fali elektromagnetycznej
atom sodu
300 m s
l 1m
8
10 s
a 10 g
4
EMO-20
fala EM dowolnego źródła
rozwiązanie
równania
falowego
dla
dowolnego
źródła
równania Maxwella w próżni
potencjały oraz pola ładunków i prądów zmiennych w czasie
E 0
B 0
B
E
0
t
E
B 0 0
0 j
t
potencjały oraz pola ładunków i prądów zmiennych w czasie
(zob.: rozdziały 10 i 11 Griffiths str 448-500)
demo apples + bamboos
rozkład ładunku i prądu
potencjały (skalarny i wektorowy)
przekształcenia cechowania
potencjały (przedwczesne oraz) opóźnione
pola E i B
potencjały quasistatyczne
(skalarny i wektorowy)
B A
E V
A = potencjał wektorowy
V = potencjał skalarny
jak skonstruować potencjały
dla pól zmiennych w czasie ?
potencjały (skalarny i wektorowy)
B A A = potencjał wektorowy
B
E
( A) Faraday
t
t
A
(E ) 0
t
A
A
E
V E
V
t
t
V = potencjał skalarny
przekształcenia cechowania
A A
V V
t
λ = dowolna funkcja skalarna
B A
A
E
V
t
cechowanie Coulomba, Lorentza …
równania Maxwella dla potencjałów A i V
równania Maxwella dla potencjałów A i V
V ( A)
t
0
2
A
V
(A 0 0 2 ) ( A 0 0
)
t
t
0 j
cechowanie Lorentza:
V
A 0 0
0
t
równanie falowe dla potencjałów A i V
V
V 0 0 2
t
0
2
A
A 0 0 2 0 j
t
2
potencjały opóźnione (przedwczesne)
t tR t R c
1
3 ( s, t R )
V (r , t ) VR (r , t )
ds
4 0
R
0
3 j ( s, t R )
A(r , t ) AR (r , t )
ds
4
R
powtórka: potencjał dipola elektrycznego
1 q q
V
(
r
)
(
)
r
40 r r
2
2
2
q - r
r r (d 2) rd cos
2
2
2
2
d
r r r [1 (d r ) cos (d 4r )]
2
2
r r [1 (d r ) cos ]
q +
1 1
1 2
[1 (d r ) cos ]
d r
r r
1 1
[1 (d 2r ) cos ]
r r
statyczny potencjał dipola elektrycznego
q -
d
q +
r
r
r
1 q q
V (r )
( )
40 r r
1 1
[1 (d 2r ) cos ]
r r
1 1 d
2 cos
r r r
1 qd
Vdip (r )
cos
2
40 r
potencjał dipola elektrycznego zależny od czasu
q -
d
q +
r
r
r
1 q q
V (r )
( )
40 r r
q(t ) q0 cos(t )
p(t ) q0 d cos(t )
ładunek oscyluje
dipol oscyluje
1 q0 cos[ (t r c)] q0 cos[ (t r c)]
V (r , t )
(
)
40
r
r
demo bambusy
applet Electric1/embox more applets 2-D (TE)
potencjał dipola elektrycznego zależny od czasu
1 q0 cos[ (t r c)] q0 cos[ (t r c)]
V (r , t )
(
)
40
r
r
q0 d cos
r
r
r
V (r , t )
{cos[ (t )]
sin[ (t )]}
2
40 r
c
c
c
0 q0 d
r
A(r , t )
sin[ (t )] zˆ
4 r
c
r ˆ
2 0 q0 d sin
E (r , t )
cos[ (t )]
4
r
c
r ˆ
2 0 q0 d sin
B(r , t )
cos[ (t )]
4 c r
c
promieniowanie dipola elektrycznego
promieniowanie dipola magnetycznego
(web.MIT.edu)
koniec
EMO-20