Physics of magnetics

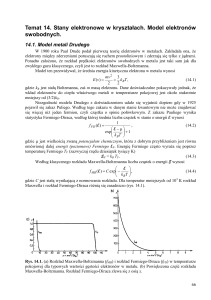
Problem: QM ω(α)
E(T)=suma n(T,α)·ω(α)=?
Zajmiemy się tylko elektronami: fermiony, N=const
N

n(T ,  ) 
  0..1024
gdzie
 n(i)  [n(i) / g (i)]  [g (i) /  ]  
i  0.. 106
i  0.. 106
i   , f (,T , EF )  n(i) / g (i)
 termodynamika
i   ,  ( )  g (i ) / 
f(ω)=funkcja rozkładu
(tutaj: T=0)
1
ω
Ef
 mech. kwantowa
ρ(ω)=funkcja gęstości stanów
ω
Funkcja gęstości stanów ρ(ω)=Δg/Δω:
V(r)  QM  ρ(ω)
opis wg QM (α)  (i)
α = 0..1024
i = 0..106
ω
ω
Δω
0
i
opis uproszczony
ωi
Δgi
ρ(ω)
2 5=ω2 5=Δg2
2,5
1 3=ω1 9=Δg1
4,5
0 1=ω0 4=Δg0
2,0
Funkcja rozkładu f(ω,T,Ef)=Δn/Δg:
T  termodynamika  f(ω,T,Ef)
dla fermionów: obowiązuje zakaz Pauliego, 0<f<1
(dla bozonów: zakaz Pauliego nie obowiązuje, 0<f)
1
f ( , T , EF )  (  EF ) / T
e
1
WAŻNE: aby wyznaczyć energię Fermiego EF (tutaj jako
parametr modelu, konieczny do obliczeń) należy tak
dobrać Ef aby doprowadzić do samouzgodnienia:
N   ni  f (i , T , EF )   (i )  
i
i
dla zadanej liczby elektronów N. Stąd EF(T) zależy od T,
choć w większości przypadków jest to słaba zależność.
Problem: QM ω(α)
E(T)=suma n(T,α)·ω(α)=?
Dla zadanej liczby elektronów N, i po ustaleniu energii
Fermiego EF, można wyliczyć energię wszystkich elektronów
E (T )   i  ni     f ( , T , EF )   ( )  d
i
Np. dla T=0 mamy EF=1 dla ω<EF, i EF=0 dla ω>EF. Ponadto w
pobliżu dna pasma (ω=0, małe N) QM daje w przybliżeniu
2 dla standardowej próbki 3D. Wówczas
ρ(ω)=Aω
E
F
E (0)    1 A   d  A  ( EF )5 / 2 /(5 / 2)
0
EF
N  1  A   d  A  ( EF )3 / 2 /(3 / 2)
0
a stąd spodziewana średnia energia pojedynczego elektronu
0<E/N< EF wynosi E/N=0,6·EF.
Strefy Brillouina
Koncepcja stref Brillouina wynika bezpośrednio z faktu, że
periodyczność V(r), charakterystyczna dla kryształu, przewiduje
rozwiązania dla energii ω w postaci ω(kx,ky,kz) jako funkcji
periodycznej wektora falowego (kx,ky,kz), np. ω(kx+2π/ax,ky,kz) =
ω(kx,ky,kz), w kierunku kx; podobnie w pozostałych kierunkach ky
i kz. Dlatego można ograniczyć zależność ω(kx,ky,kz) do jednego
periodu; zazwyczaj jest to przedział od (-π/a) do (π/a), czyli do
tzw. (pierwszej) strefy Brillouina.
ky
+π/ay
x = punkty
x
x
równoważne
(o tej samej
-π/ax
+π/ax
kx
energii ω)
-π/ay
x
x
Strefy Brillouina i kwantyzacja,
„ciecz Fermiego”
Można udowodnić, że (kx,ky,kz) mogą przyjmować tylko
dyskretne wartości, a stąd energie ω są również dyskretne.
k x  nx  2 /( N x ax ), nx   N x / 2..N x / 2
gdzie Nx jest liczbą atomów wzdłuż osi x-ów kryształu. Ten
zakres zmienności nx odpowiada zakresowi kx od (-π/ax) do
(π/ax). Całkowita liczba dozwolonych energii wynosi liczbie
atomów Na= Nx·Ny·Nz, czego należało oczekiwać. Np. dla danej
liczby elektronów N=0,1·Na mamy
ky
+π/ay
-π/ax
+π/ax
-π/ay
kx
Powierzchnia Fermiego dla T=0
Szczegółowy opis energii ω w paśmie kryształu 0<ω<W jest
dany przez zależność ω(kx,ky,kz), od wektora falowego (kx,ky,kz).
Zgodnie z zasadą minimum energii, N elektronów zajmie
możliwie (zakaz Pauliego!) najniższe z dozwolonych energii w
pobliżu dna pasma dla k=0. Oznacza to, że jeżeli wyznaczymy
powierzchnię stałej energii ω(kx,ky,kz)=EF, to wszystkie
dozwolone stany (kx,ky,kz) wewnątrz tej powierzchni Fermiego
będą obsadzone. Dla ω(kx,ky,kz) = ω(k) będzie to sfera. W
ogólności,
 np. w modelu TBM, powierzchnia Fermiego nie jest
sferą,  (k )  2  {t x [1  cos(k x ax )]  t y [1  cos(k y a y )]  t z [1  cos(k z a z / 2)]}

 ( k )  t x  ( k x a x ) 2  t y  ( k y a y ) 2  t z  ( k z az ) 2
Jednak dla N << Na
i dla txax2 = tyay2 = tzaz2 powierzchnia Fermiego jest sferą.
Powierzchnia Fermiego dla T>0
Ogólna koncepcja przypadku T>0 polega na uwzględnieniu
faktu, że zasada minimum energii ω(α) jako kryterium
obsadzenia stanu α, n(α)=1, dla T=0 musi być zastąpiona
prawdopodobieństwem p obsadzenia tego stanu. Ponieważ
funkcja rozkładu zdefiniowana przez f(ω,T,Ef)=Δn/Δg jest
właśnie prawdopodobieństwem p, to algorytm brzmi:
dla każdego stanu α
licz ω(α)  f=1/[exp(ω-Ef)/T + 1]
obsadź stan n(α)=1 z prawdopodobieństwem f,
else n(α)=0
Praktycznie f=1 dla ω<Ef, f=0 dla ω>Ef, i jedynie dla ω w
pobliżu energii Fermiego Ef, ściślej dla Ef -T < ω < Ef +T, mamy
obszar przejściowy, czyli rozmycie granicy między stanami
zajętymi i pustymi. (Jest to też argument na rzecz użyteczności
pojęcia energii Fermiego – tylko elektrony bliskie Ef mogą być
mobilne, elektrony o mniejszych energiach są zamrożone z
powodu zakazu Pauliego.)
Gęstości stanów ρ(ω)=Δg/Δω dla
próbek o innych wymiarach D
Zazwyczaj krzyształ jest identyfikowany jako 3-wymiarowa
próbka D=3. Mamy też próbki o niższym wymiarze, np. D=2
(cienkie warstwy), D=1 (białka DNA, wiskersy, polimery).
Pokażemy, jak w granicy N << Na (jak półprzewodniki)
funkcja ρ(ω) jest modyfikowana przez wymiar D:
  k 2   ( )  k D2 ,  ( )  A D / 21
Podstawą tego wyniku jest założenie ω ~ k2 słuszne dla
N << Na, oraz warunki kwantyzacji wektora falowego
(kx,ky,kz) który wyznacza jednorodny rozkład dozwolonych
stanów w przestrzeni wektora falowego.
Energia E(0)/N dla próbek o innych
wymiarach D dla w granicy N<<Na
W temperaturze T=0, i dla ω ~ k2, mamy
 ( )  A
D / 2 1
 ( )  A
(T  0)  E  
EF
0
D / 2 1
(T  0)  N  
EF
0
i wówczas
E
D

 EF
N D2
A
D / 2 1
d   ( ) 
EF
D / 2 1
d   ( ) 
A
D/2
EF
D/2
Model silnego wiązania dla innych
struktur krystalograficznych
Model TBM pozwala obliczyć analityczne relacje ω(kx,ky,kz) dla
kilku typowych struktur krystalograficznych dla tx=ty=tz, co
odpowiada strukturom regularnym ax=ax=az.

 (k )  0  2t  [cos( k x a)  cos(k y a)  cos(k z a)], SC, Z  6

 (k )  0  8t  [cos( k x a / 2) cos(k y a / 2) cos(k z a / 2)], BCC ( Fe), Z  8

 (k )  0  4t  [cos( k x a / 2) cos(k y a / 2)  ...], FCC( Ni), Z  12
SC = Simple Cubic, struktura regularna
BCC = Body Centered Cubic, struktura regularna przestrzennie
centrowana
FCC = Face Centered Cubic, struktura regularna
powierzchniowo centrowana
Model silnego wiązania dla innych
struktur krystalograficznych
We wszystkich SC, BCC i FCC strukturach Z oznacza tzw liczbę
koordynacyjną, czyli liczbę najbliższych sąsiadów Z= 6, 8, 12
odpowiednio. Parametr t ~ a–5 dla stałej sieciowej a wynosi zero
dla fazy gazowej (gdy a zmierza do nieskończoności, atomy,
jedna energia zamiast pasma o szerokości W). Wzory analityczne
przewidują W=2Zt dla wszystkich struktur oraz w granicy
N << Na przybliżoną energię
ω=t(ka)2.
Wykładnik (-5) wynika z ogólniejszej zależności t(a) dla pasma
typu określonego przez orbitalną liczbę kwantową:
dla l = 0,1,2,3,...
czyli s,p,d,f,...
mamy t ~ a–(g/2) = a–(2l+1).