1.
Napisz wzór funkcji liniowej f, której wykres przechodzi przez punkt A(–
cos =
2.
6 , –2) i jest nachylony do osi OX pod takim kątem , że
3
. Podaj wzór proporcjonalności prostej, której wykres jest prostopadły do wykresu funkcji f.
5
a) Napisz wzór nieparzystej funkcji liniowej, której wykres jest nachylony do dodatniej półosi osi OX pod kątem 120 0 .
b) Jaką wartość musi mieć parametr k, aby prosta y= k x+2 przecinała wykres funkcji z punktu a) pod katem prostym.
3.
Punkty A(2, 0) i B(0, 4) należą do wykresu funkcji liniowej f(x) = (3m – 2k)x + 2k + m.
a) Wyznacz k i m. b) Napisz równanie proporcjonalności prostej, której wykres jest równoległy do wykresu funkcji f.
c) Wyznacz miejsce zerowe funkcji y = g(x), gdzie g(x) = f(2x + 1) – 3.
4. Wyznacz liczbę a, dla której trzy proste k: y = 2x – 3, l: y = –x oraz m: y = –3x + a przecinają się w jednym punkcie.
5.
Dla jakich wartości parametru m wykresy funkcji f(x) = ||m + 2| – 1|x + 2m i g(x) =
1
x + 1 są prostopadłe?
2
6. Dla jakich wartości parametru m wykresy funkcji f(x) = ||m – 1| + 2|x – 3m i g(x) = 7x – 5 są równoległe?
7. Dana jest funkcja liniowa f(x) = (m + 1)x + m2 – 1.
a) Wyznacz wartość parametru m (m R), dla którego funkcja f ma nieskończenie wiele miejsc zerowych.
b) Wyznacz wartość parametru m, dla którego miejsce zerowe funkcji f należy do przedziału 2m – 2, 2m + 4.
8.
Dana jest funkcja o wzorze f(x) = 2|x – 1| +
x 2 4x 4 .
a) Napisz wzór funkcji nie używając symbolu wartości bezwzględnej i pierwiastka kwadratowego.
b) Narysuj wykres tej funkcji. c) Zbadaj liczbę rozwiązań równania f(x) = k, kR, ze względu na wartość parametru k.
9.
Narysuj wykres funkcji
f (x)
parametru k.
10. Naszkicuj wykres funkcji f(x) =
x2 x
1 i na jego podstawie zbadaj liczbę rozwiązań równania f(x)=k w zależności od wartości
x 1
x 3
· x + 3, a następnie określ liczbę rozwiązań równania f(|x|) = p w zależności od wartości
|3 x |
parametru p (p R).
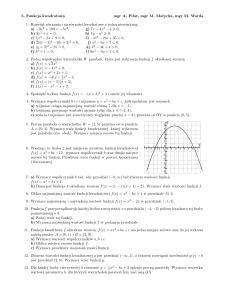
11. Opisz za pomocą układu nierówności zbiór przedstawiony na rysunku
12. W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów, których współrzędne spełniają układ nierówności
| y | 2
.
x 1
y 4 2x
13. Zaznacz na płaszczyźnie zbiór A B, jeśli:
A={(x,y): x R, y R, 2x-y<4}
B={(x,y): x R, y R, x+y-1 0}
14. Dane są zbiory A = {x: x R |2x + 1| = 2x + 1} i B = {x: x R |15 – 3x| < 3}. Przedstaw graficznie zbiór
C = {(a, b): a A b B}.
15. Samochód zużywa średnio 7 litrów benzyny na 100 km. W jego baku znajduje się 21 litrów paliwa. Napisz wzór funkcji opisującej
liczbę litrów benzyny, jaka pozostała w baku w zależności od liczby przejechanych kilometrów. Wprowadź oznaczenia: a – liczba
przejechanych kilometrów, b – liczba litrów paliwa. Na ile kilometrów jazdy wystarczy paliwo znajdujące się w baku?
16. Jeden z pracowników firmy SARATON otrzymuje stałą pensję miesięczną za 168 przepracowanych godzin oraz dodatkowe
wynagrodzenie za nadgodziny. Stawka za godzinę nadliczbową jest o 50% większa niż za godzinę etatową. W styczniu pracownik ten
miał 8 nadgodzin i otrzymał razem 2700 zł. Oblicz stawkę za godzinę nadliczbową oraz stawkę za godzinę etatową. Napisz wzór
funkcji wyrażającej wynagrodzenie pracownika w zależności od liczby przepracowanych godzin nadliczbowych.
17. Rozwiąż nierówności i równanie a) x 3 4x 2 4x 1 1
b) x 3 4x 2 4x 1 1
c) 4 x 2x 8 x 2 16 2 1 x 0
2
18. Wyznacz dziedzinę funkcji:
f ( x ) 1 x 3 4x 2 4x 1
19. Wyznacz miejsca zerowe funkcji: f(x)=
x 3 4x 2 4x 1 1
5x 3y 2k 18
20. Dla jakiej wartości parametru k (k R) rozwiązaniem układu równań
jest para liczb (x, y) spełniająca warunek
2x y 3k 5
|y| – |x| 0?
4x 5y t 1 jest para liczb o przeciwnych znakach?
2 x 3 y t 3
21. Dla jakich wartości parametru t rozwiązaniem układu równań
x y m 1
2x y 3 m
jest parą liczb ujemnych?
x 2 y 5m 5
3x y m 6
jest para liczb spełniających warunek |𝑥| − |𝑦| <
22. Dla jakich wartości parametru m rozwiązaniem układu równań
23. Dla jakich wartości parametru m rozwiązaniem układu równań
1?
24. Określ liczbę rozwiązań równania liniowego a2x + 3 = 9x – a w zależności od wartości parametru a. W przypadku istnienia rozwiązania
wyznacz je.
25. Zaznacz na płaszczyźnie zbiór A = {(x, y): xR yR
x = 3 |2y – 5| 1}, gdzie symbol a oznacza największą liczbę całkowitą
nie większą niż a.
26. Na płaszczyźnie z prostokątnym układem współrzędnych zilustruj zbiór punktów, których współrzędne spełniają nierówność:
|y – 1| |x – 2| + 1.